Objects in the expressions for Lagrangian terms

Each symbol which may appear in algebraic expressions (names of parameters, fields, etc) has a fixed order of indices and their types. If this object is used in any expression, one should write its indices in the same order as they were defined when the object has been declared.

Besides the types of indices corresponding to the color $SU(3)$ group: color c3 (color triplet), color c3b (color antitriplet) and color c8 (color octet) described in the previous example, there are default types of indices for Lorentz group: vector, spinor and cspinor (antispinor). User can also declare new types of indices corresponding to the symmetries other than color $SU(3)$ group. In this case any object (say, particle) may have indices related to this new group. This possibility will be described in Section 8.

If an index appears twice in some monomial of an expression, LanHEP assumes summation over this index. Types of such indices must allow the contraction, i.e. they should be one of the pairs: spinor and cspinor, two vector, color c3 and color c3b, two color c8.

In general the following objects are available to appear in the expressions for a Lagrangian: integers and identifiers of parameters, particles, specials, let-substitutions and arrays.

There are also predefined symbols i, denoting imaginary unit $i$ ($i^2=-1$) and Sqrt2, which is a parameter with value $\sqrt{2}$.

Parameters

Parameters are scalar objects (i.e. they have no indices). Parameters denote coupling constants, masses and widths of particles, etc. To introduce a new parameter one should use the parameter statement, which has the generic form

parameter name=value:comment.

• name is an identifier of newly created parameter.
• value is an integer or floating point number or an expression. One can use previously declared parameters and integers joined by standard arithmetical operators '+', '-', '*', '/', and '**' (power).
• comment is an optional comment to clarify the meaning of parameter, it is used in CompHEP help windows. Comment has to be a string constant, so if it contains blank spaces or other special characters, it must be quoted (see Section 3).

In the extression for parameters one can use functions sqrt, pow, sin, asin, cos, acos, tan, atan, atan2, fabs (same as in C programming language). One can add new functions through the use of the statement

external_func(function, arity).

Arity is the number of arguments of the function. If this function is absent in the standard C library, it should be written in C and added to the library file usrlib.a in the CompHEP working directory.

Particles

Particles are objects to denote physical particles. They may have indices. It is possible to use three statements to declare a new particle, at the same time the second and the third statements define the corresponding Lorentz index:

scalar P/aP:(options).
spinor P/aP:(options).
vector P/aP:(options).

P and aP are identifiers of particle and antiparticle. In the case of truly neutral particles (when antiparticle is identical to the particle itself) one should use the form P/P with identical names for particle and antiparticle.

It is possible to write only the particle name, e.g.

scalar P:(options).

In this case the name of corresponding antiparticle is generated automatically. It satisfies the usual CompHEP convention, when the name of antiparticle differs from particle by altering the case of the first letter. So for electron name e1 automatically generated antiparticle name will be E1. If the name contains symbol '+' it is replaced by '-' and vice versa.

The option is comma-separated list of options for a declared particle, and it may include the following items:

• the first element in this list must be the full name of the particle, (e.g. electron and photon in our example.) Full name is a string constant, so it should be quoted if it contains blanks, etc.
• mass param=value defines the mass of the particle. Here param is an identifier of a new parameter, which is used to denote the mass; value is its value, it has the same syntax as in the parameter statement, comment for this new parameter being generated automatically. If this option omitted, the mass is assumed to be zero.
• width param=value declares the width of the particle. It has the same syntax as for mass option.
• itype is a type of index of some symmetry; one can use default index types for color $SU(3)$ group (see QCD example in Section 2). It is possible to use user-defined index types (see Section 8) and Lorentz group indices vector, spinor, cspinor.
• left or right says that the massless spinor particle is an eigenstate of $(1-\gamma^5)/2$ or $(1+\gamma^5)/2$ projectors, so this fermion is left-handed or right-handed.
• gauge declares the vector particle as a gauge boson. This option generates the corresponding ghosts and goldstone bosons names for the named particle (see below).

When a particle name is used in any expression (in Lagrangian terms), one should remember that the first index is either a vector or a spinor (if this particle is not a Lorentz scalar). Then the indices follow in the same order as index types in the options list. So, in the case of quark declaration (see the QCD example) the first index is spinor, and the second one is color triplet.

There are several functions taking particle name as an argument which can be used in algebraic expressions. These functions are replaced with auxiliary particle names, which are generated automatically.

• Ghost field names in gauge theories are generated by the functions ghost(name) $\rightarrow$ 'name.c' and ccghost(name) $\rightarrow$ 'name.C' (see for instance Table 1). Here and below name is the name of the corresponding gauge boson.
• Goldstone boson field name in the t'Hooft-Feynman gauge is generated by the function gsb(name) $\rightarrow$ 'name.f'.
• The function anti(name) generates antiparticle name for the particle name.
• The name for a charge conjugate spinor particle $\psi^c=C\bar{\psi}{}^T$ is generated by the function cc(name) $\rightarrow$ 'name.c'. Charge conjugate fermion has the same indices types and ordering, however index of spinor type is replaced by the index type cspinor and vice versa.
• vev(expr) is used in the Lagrangian for vacuum expectation values. Function vev ensures that deriv*vev(expr) is zero. In other words, vev function forces LanHEP to treat expr as a scalar particle which will be replaced by expr in Feynman rules.

Specials

Besides parameters and particles other indexed such as $\gamma$-matrices, group structure constants, etc may appear in the Lagrangian terms. We refer such objects as specials.

Predefined specials of the Lorentz group are:

• gamma stands for the $\gamma^\mu$-matrices. It has three indices of spinor, cspinor and vector types.
• gamma5 denotes $\gamma^5$ matrix. It has two indices of spinor and cspinor types.
• moment has one index of vector type. At the stage of Feynman rules generation this symbol is replaced by the particle moment.
• deriv is replaced by $-ip_\mu$, where $p_\mu$ is the particle moment. It has one vector index. Note that deriv*A*B means $(\partial A)B$, not $\partial (AB)$.
• For the derivative of a product, derivp(expr) can be used. derivp(A*B) is equivalent to deriv*A*B+A*deriv*B.

Specials of the color $SU(3)$ group are:

• lambda denotes Gell-Mann $\lambda$-matrices. It has three indices: color c3, color c3b and color c8.
• f_SU3 is the $SU(3)$ structure constant. It has three indices of color c8 type.
• eps_c3 and eps_c3b are antisymmetric tensors. The first has 3 indices of the type color c3, and the second 3 color c3b indices.

Note that for specials the order of indices types is fixed.

Users can declare new specials with the help of a facility defined in Section 8 to introduce user-defined indices types.

Let-substitutions

LanHEP allows the user to introduce new symbols and then substitute them in Lagrangian terms by some expressions. Substitution has the generic form

let name=expr.

where name is the identifier of newly defined object. The expression has the same structure as those in Lagrangian terms, however here expression may have free (non-contracted) indices.

Typical example of using a substitution rule is a definition of the QED covariant derivative as

let Deriv^mu=deriv^mu + i*ee*A^mu.

corresponding to $D_\mu=\partial_\mu + ig_eA_\mu$.

More complicated example is the declaration $\sigma^{\mu\nu} \equiv i(\gamma^\mu\gamma^\nu-\gamma^\nu\gamma^\mu)/2$ matrices:

let sigma^a^b^mu^nu = i*(gamma^a^c^mu*gamma^c^b^nu
- gamma^a^c^nu*gamma^c^b^mu)/2.

Note that the order of indices types of new symbol is fixed by the declaration. So, first two indices of sigma after this declaration are spinor and antispinor, third and fourth are vector indices.

Arrays

LanHEP allows to define components of indexed objects. In this case, contraction of indices will be performed as an explicit sum of products of the corresponding components.

An object with explicit components has to be written as

{expr1, expr2 ..., exprN }^i

where expressions correspond to components. All indices of components (if present) have to be written at the each component, and the index numbering components has to be written after closing curly bracket. Of course, all the components must have the same types of free (non-contracted) indices.

Arrays are usually applied for the definition of multiplets and matrices corresponding to broken symmetries.

Typical example of arrays usage is a declaration of electron-neutrino isospin doublet l1 (and antidoublet L1)

let l1^a^I = { n1^a, e1^a}^I, L1^a^I = { N1^a, E1^a}^I.

Here we suppose that n1 was declared as the spinor particle (neutrino), with the antiparticle name N1.

Note that the functions anti and cc can be applied also to the multiplets, so the construction

let l1^a^I = { n1^a, e1^a}^I, L1^a^I = anti(l1)^a^I.

is possible.

Matrices can be represented as arrays which have other arrays as components. However, it is more convenient to declare them with dummy indices, see Section 5.4 (the same is correct for multiplets also).

It is possible also to use arrays directly in the Lagrangian, rather than only in the declaration of let-substitution.

When LanHEP is launched, it has already declared some frequently used matrices. They are:

• tau1, tau2, tau3 are $\tau$-matrices $\tau_1, \tau_2, \tau_3$:
  
  $$\tau^1 = \left(\begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array} ... ...= \left(\begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \right);$$
  
  

• tau is a vector $\vec{\tau}=(\tau_1, \tau_2, \tau_3)$;
• taup and taum are matrices $\tau^\pm=(\tau^1\pm i\tau^2)/ \sqrt{2}$;
• taupm is a vector $(\tau^+, \tau^3, \tau^-)$;
• eps is the antisymmetrical tensor $\varepsilon$ ( $\varepsilon^{123}=1$);
• Tau1, Tau2, Tau3 are generators of $SU(2)$ group adjoint representation (3-dimensional analog of $\tau$-matrices) $T^1, T^2, T^3$ with commutative relations $[T_i,T_j]=-i\epsilon_{ijk}T_k$:
  
  $$T^1= \frac{1}{\sqrt{2}} \left(\begin{array}{rrr} 0 & -1 & 0 ... ...rr} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{array} \right);$$
  
  

• Taup and Taum corresponds to $T^\pm=(T^1\pm iT^2)/ \sqrt{2}$;
• Taupm is a vector $\vec{T}=(T^+, T^3, T^-)$.

Two-component notation for fermions

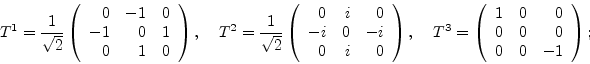
It is possible to write the Lagrangian using two-component notation for fermions. The connection between two-component and four-component notations is summarized by the following relations:

$$\psi=\left(\begin{array}{c} \xi \\ \bar\eta \end{array} \r... ...=\left(\begin{array}{c} \xi \\ \bar\eta \end{array} \right)^T.$$

If the user has declared a spinor particle p (with antiparticle P), the LanHEP notation for its components is:

$\xi$	$\rightarrow$	up(p)
$\bar\eta$	$\rightarrow$	down(p)
$\eta$	$\rightarrow$	up(cc(p)) or up(P)
$\bar\xi$	$\rightarrow$	down(cc(p)) or down(P)

To use the four-vector $\bar\sigma^\mu$ one should use the statement

special sigma:(spinor2,spinor2,vector).

Note that the sigma object is not defined by default, thus the above statement is required. It is possible also to use another name instead of sigma (this object can be recognized by LanHEP by the types of its indices).

LanHEP uses the following rules to convert the two-component fermions to four-component ones (we use $P_{R,L}=(1\pm\gamma^5)/2$):

$\eta_1\xi_2=\bar\psi_1P_L\psi_2$	up(P1)*up(p2)	$\rightarrow$	P1*(1-gamma5)/2*p2
$\bar\eta_1\bar\xi_2=\bar\psi_1P_R\psi_2$	down(P1)*down(p2)	$\rightarrow$	P1*(1+gamma5)/2*p2
$\xi_1\xi_2=\bar\psi_1^cP_L\psi_2$	up(p1)*up(p2)	$\rightarrow$	cc(p1)*(1-gamma5)/2*p2
$\bar\xi_1\bar\xi_2=\bar\psi_1P_R\psi_2^c$	down(P1)*down(P2)	$\rightarrow$	P1*(1+gamma5)/2*cc(P2)
$\xi_1\eta_2=\bar\psi_1^cP_L\psi_2^c$	up(p1)*up(P2)	$\rightarrow$	cc(p1)*(1-gamma5)/2*cc(P2)
$\bar\xi_1\bar\eta_2=\bar\psi_1^cP_R\psi_2^c$	down(p1)*down(P2)	$\rightarrow$	cc(p1)*(1+gamma5)/2*cc(P2)
$\eta_1\eta_2=\bar\psi_1P_L\psi_2^c$	up(P1)*up(P2)	$\rightarrow$	P1*(1-gamma5)/2*cc(P2)
$\bar\eta_1\bar\eta_2=\bar\psi_1^cP_R\psi_2$	down(p1)*down(p2)	$\rightarrow$	cc(p1)*(1+gamma5)/2*p2
$\bar\xi_1\sigma^\mu\xi_2=\bar\psi_1\gamma^\mu P_L\psi_2$	down(P1)*sigma*up(p2)	$\rightarrow$	P1*gamma*(1-gamma5)/2*p2
$\bar\eta_1\sigma^\mu\eta_2=\bar\psi_1^c\gamma^\mu P_L\psi_2^c$	down(p1)*sigma*up(P2)	$\rightarrow$	cc(p1)*gamma*(1-gamma5)/2*cc(P2)