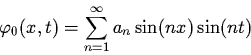Construction of doubly periodic solutions
via the Poincare-Lindstedt method
in the case of massless 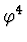 theory
theory
Sergey Yu. Vernov
Institute for Nuclear Physics of Moscow State
University,
Vorobievy Gory, Moscow, 119899, Russia
Abstract
Doubly periodic solutions for the Lagrange-Euler equation
of the (1+1)-dimensional scalar 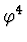 theory are studied. Provided that nonlinear term is small, the Poincare-Lindstedt
method is used to find asymptotic solutions in the standing wave form.
If the mass of the scalar field is zero, then the standard zero approximation:
theory are studied. Provided that nonlinear term is small, the Poincare-Lindstedt
method is used to find asymptotic solutions in the standing wave form.
If the mass of the scalar field is zero, then the standard zero approximation:
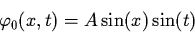
doesn't allow to construct a uniform expansion even to
the first order. Such expansion can be found if and only if a zero approximation
contains infinite number of harmonics:
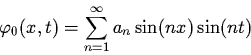 with the coefficients an obeying some infinite
system of algebraic nonlinear equations. An approximate solution
of this system have been found by the computer algebra system REDUCE. It
is proved that using the Jacobi elliptic function cn as a zero approximation,
one can find an exact solution of this system and construct a uniform expansion,
containing only doubly periodic functions in the standing wave form, both
to the first and to the second order.
with the coefficients an obeying some infinite
system of algebraic nonlinear equations. An approximate solution
of this system have been found by the computer algebra system REDUCE. It
is proved that using the Jacobi elliptic function cn as a zero approximation,
one can find an exact solution of this system and construct a uniform expansion,
containing only doubly periodic functions in the standing wave form, both
to the first and to the second order.
root
1998-07-29
![]() theory are studied. Provided that nonlinear term is small, the Poincare-Lindstedt
method is used to find asymptotic solutions in the standing wave form.
If the mass of the scalar field is zero, then the standard zero approximation:
theory are studied. Provided that nonlinear term is small, the Poincare-Lindstedt
method is used to find asymptotic solutions in the standing wave form.
If the mass of the scalar field is zero, then the standard zero approximation: