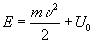
Задача
9. Исследовать движение электрона через потенциальный барьер прямоугольной формы и бесконечной протяженности высотой
. Получить значения коэффициентов отражения 
и прозрачности (прохождения) D. Принять, что энергия электрона больше высоты потенциального барьера. Найти 
и D для следующих отношений энергий: 
10; 2; 1,25; 1.
Решение.
Пусть на пути электрона, движущегося в положительном направлении оси
, встречается потенциальный барьер бесконечной ширины и постоянной высоты 
(рис.3), то есть при 
< 0 
- область I, при 
- область II.
По условию задачи 
>
. Если рассматривать электрон как частицу, подчиняющуюся классической механике, то он обязательно прейдет из области I в область II. Попадая в область потенциального барьера на границе I и II , электрон преодолевает этот барьер, так как
его полная энергия
>, и продолжает свое движение в области II с уменьшенной кинетической энергией -. Действительно, из Рис.5
закона сохранения энергии
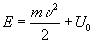
следует, что скорость частицы над потенциальным барьером должна быть равна в рассматриваемом случае
,
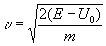
причем при
скорость равна нулю 
, т.е. частица останавливается.
В квантовой механике электрон обладает волновыми свойствами и описывается волновой функцией. Учитывая, что интенсивность любого волнового процесса прямо пропорциональна квадрату амплитуды волны и скорости ее распространения, коэффициент
отражения 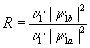определяется из соотношения
(1)
Коэффициент прозрачности
D равен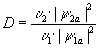 
(2)
В соотношениях (1), (2) величины
, 
имеют физический смысл соответственно плотности вероятности обнаружения частицы, движущейся соответственно в прямом и обратном направлениях в области I и в прямом в области II, 
и 
- скорости частицы в областях I и II. Согласно закону сохранения числа частиц, если нет поглощения,
. (3)
Задача
o нахождении коэффициентов отражения
или прохождения 
далее сводится к решению уравнений Шредингера для областей I и II с соответствующими условиями на границе барьера. Пусть поведение электрона в области I описывается волновой функцией 
, а в области II функцией 
. Составим уравнение Шредингера для областей I и II.
Для области I, где
, 
имеем
; (5)
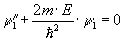
а для области II, где
, 
получаем
(6)
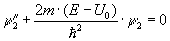
Исходя из условий непрерывности
волновой функции и ее первой производной запишем условия на границе барьера в точке
:
(7)
Учитывая, что
; 
, где 
и 
- волновые числа, перепишем уравнения (5) и (6) в виде:
; (8)
. (9)
Решение уравнения (8) будем искать в виде
, (10)
где
- амплитуда падающей волны; 
- амплитуда отраженной от барьера волны. Соответственно решением уравнения (9) будет волновая функция
, (11)
где
- амплитуда волны, распространяющейся в направлении положительных 
в области II; 
- амплитуда волны, распространяющейся в направлении отрицательных . По отношению к волне с амплитудой эта волна является отраженной. По условию задачи для барьера бесконечной ширины отражения в области II не происходит, т.е. 
. Тогда
. (12)
Амплитуды
и 
находятся из граничных условий (7). Из условия равенства волновых функций при 
найдем
+=. (13)
Вычислив производные
и 
и, используя их равенство при 
, составим второе уравнение для двух неизвестных и :
. (14)
Решая систему уравнений (13) и (14), найдем
. (15)
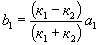
Подставляя
в выражение (1), найдем величину 
:
. (16)
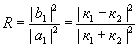
Учитывая, что
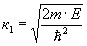и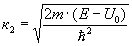 
, получим
. (17)
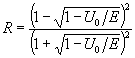
Коэффициент прохождения
D можно определить из соотношения (3). В таблице приведены значения для заданных отношений 
:
|
|
10 |
2 |
1,25 |
1 |
|
|
0,0007 |
0,0296 |
0,1459 |
1,0000 |
Анализируя полученные результаты получаем, что при
>1 наблюдается частичное отражение частиц от границы потенциального барьера, а в случае 
- полное внутреннее отражение. Эти результаты не имеют аналога в классической физике.
