,Задача 7.
Электрон в атоме водорода находится в состоянии, описываемом радиальной волновой функцией,
где 
и 
- некоторые постоянные. Найти энергию электрона в этом состоянии.
Решение.
Волновая функция, представляющая состояние с некоторой энергией, является решением уравнения (2). Подставим волновую функцию в уравнение (2). Поскольку заданная волновая функция не зависит от углов, в операторе Лапласа останутся только производные по 
. Получим уравнение:
.
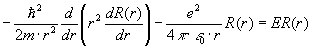
Подставив сюда заданную волновую функцию и произведя дифференцирование, придем к уравнению:
или, сгруппировав члены по степеням 
.
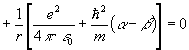
Поскольку при подстановке решения в уравнение должно получаться тождество, соотношение должно обращаться в 0 при любом . Это возможно только, если коэффициенты при всех степенях равны нулю:
; (1)
; (2)
. (3)
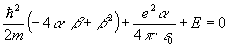
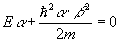
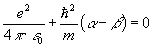
Из уравнения (2) имеем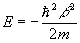 
. Подставив это выражение в уравнение (1), получаем 
Подставив это выражение в соотношения для энергии, получим:
.
Полученное выражение можно записать в виде: 
Сравнивая с соотношением (9), находим, что найденное значение энергии соответствует уровню 