Getting started with LanHEP

QED

We start with a simple exercise, illustrating the main ideas and features of LanHEP. The first physical model is Quantum Electrodynamics.

Figure 1: LanHEP input file for the generation of QED Feynman rules

The QED Lagrangian is

$${\cal L}_{QED}=-\frac{1}{4}F_{\mu\nu} F^{\mu\nu} + \bar e \gamma^\mu(i\partial_\mu + g_e A_\mu)e - m\bar e e$$

and the gauge fixing term in Feynman gauge has the form

$${\cal L}_{GF}=-\frac{1}{2}(\partial_\mu A^\mu)^2.$$

Here $e(x)$ is the spinor electron-positron field, $m$ is the electron mass, $A_\mu(x)$ is the vector photon field, $F^{\mu\nu}=\partial_\mu A^\nu-\partial_\nu A^\mu$, and $g_e$ is the elementary electric charge.

The LanHEP input file to generate the Feynman rules for QED is shown in Fig. 1.

First of all, the input file consists of statements. Each statement begins with one of the reserved keywords and ends by a full-stop '.' symbol.

First line says that this is a model with the name QED and number 1. This information is supplied for CompHEP, the name QED will be displayed in its list of models. In CompHEP package each model is described by four files: 'varsN.mdl', 'funcN.mdl', 'prtclsN.mdl', 'lgrngnN.mdl' , where N is the very number specified in the model statement.

The model statement stands first in the input file. If this statement is absent, LanHEP does not generate the four standard CompHEP files, but just builds the model and prints a diagnostic, if errors are found.

The second line in the input file contains declaration of the model parameter, denoting elementary electric charge $g_e$ as ee. For each parameter used in the model one should declare its numeric value and an optional comment (it is also used in CompHEP menus).

The next two lines declare particles. Statement names spinor, vector correspond to the particle spin. So, we declare electron denoted by e1 (the corresponding antiparticle name is E1) and photon denoted by A (with antiparticle name being A, since the antiparticle for photon is identical to particle).

After the particle name we give in brackets some options. The first one is the full name of the particle, used in CompHEP; the second option declares the mass of this particle.

The let statement in the next line declares the substitution rule for symbol F.

Predefined name deriv, which is reserved for the derivative $\frac{\partial} {\partial x}$, will be replaced after the Fourier transformation by the momentum of the particle multiplied by $-i$.

The rest of the lines describe terms in the Lagrangian. Here the reserved name gamma denotes Dirac's $\gamma$-matrices.

One can see that the indices are written separated with the caret symbol '^'. Note that in the last two lines we have omitted indices. It means that LanHEP restores omitted indices automatically. Really, one can type the last term in the full format:

lterm ee*E1^a*gamma^a^b^mu*A^mu*e1^b.

It corresponds to $g_e \bar e_a \gamma^\mu_{ab} e_b A_\mu$ with all indices written. Note that the order of objects in the monomial is important to restore indices automatically.

QCD

Now let us consider the case of Quantum Chromodynamics. The Lagrangian for the gluon fields reads

$$L_{YM} = -\frac{1}{4}F^{a\mu\nu}F^a_{\mu\nu},$$

where

$$F^a_{\mu\nu}=\partial_\mu G^a_\nu-\partial_\nu G^a_\mu- g_s f^{abc}G^b_\mu G^c_\nu,$$

$G^a_\mu(x)$ is the gluon field, $g_s$ is the strong coupling constant and $f^{abc}$ are purely imaginary structure constants of the $SU(3)$ color group.

The quark kinetic term and its interaction with the gluon has the form

$$L_F = \bar q_i \gamma^\mu \partial_\mu q_i + g_s \lambda^a_{ij} \bar q_i\gamma^\mu q_j G_\mu^c,$$

where $\lambda^a_{ij}$ are Gell-Mann matrices.

Gauge fixing terms in Feynman gauge together with the corresponding Faddev-Popov ghost term are

$$-\frac{1}{2}(\partial_\mu G^\mu_a)^2 + ig_s f^{abc} \bar c^a G^b_\mu \partial^\mu c^c,$$

where $(c, \bar c)$ are unphysical ghost fields.

The corresponding LanHEP input file is shown in Fig. 2.

Figure 2: Input file for the generation of QCD Feynman rules

Table 1: QCD Feynman rules generated by LanHEP in LaTeX output format

Fields in the vertex				Variational derivative of Lagrangian by fields
${G}_{\mu p }$	${\bar\eta^G}_{q }$	${\eta^G}_{r }$		$- g_s p_3^\mu f_{p q r}$
${\bar q}_{a p }$	${q}_{b q }$	${G}_{\mu r }$		$g_s \gamma_{a b}^\mu \lambda_{p q}^r$
${G}_{\mu p }$	${G}_{\nu q }$	${G}_{\rho r }$		$g_s f_{p q r} \big(p_3^\nu g^{\mu \rho} -p_2^\rho g^{\mu \nu} -p_3^\mu g^{\nu \rho} +p_1^\rho g^{\mu \nu} +p_2^\mu g^{\nu \rho} -p_1^\nu g^{\mu \rho} \big)$
${G}_{\mu p }$	${G}_{\nu q }$	${G}_{\rho r }$	${G}_{\sigma s }$	$g_s^2 \big(g^{\mu \rho} g^{\nu \sigma} f_{p q t} f_{r s t} -g^{\mu \sigma} g^{\nu \rho} f_{p q t} f_{r s t} +g^{\mu \nu} g^{\rho \sigma} f_{p r t} f_{q s t}$
				$+g^{\mu \nu} g^{\rho \sigma} f_{p s t} f_{q r t} -g^{\mu \sigma} g^{\nu \rho} f_{p r t} f_{q s t} -g^{\mu \rho} g^{\nu \sigma} f_{p s t} f_{q r t} \big)$

Since QCD uses objects with color indices, one has to declare the indices of these objects. There are three types of color indices supported by LanHEP. These types are referred as color c3 (color triplets), color c3b (color antitriplets), and color c8 (color octets). One can see that color c3 index type appears among the options in the quark q declaration, and the color c8 one in the gluon G declaration. Antiquark Q has got color index of type color c3b as antiparticle to quark. LanHEP allows contraction of an index of type color c3 only with another index of type color c3b, and two indices of type color c8. Of course, in Lagrangian terms each index has to be contracted with its partner, since Lagrangian has to be a scalar.

LanHEP allows also to use in the Lagrangian terms a predefined symbol lambda with the three indices of types color c3, color c3b, color c8 corresponding to Gell-Mann $\lambda$-matrices. Symbol f_SU3 denotes the structure constant $f^{abc}$ of color $SU(3)$ group (all three indices have the type color c8).

Option gauge in the declaration of G allows to use names ghost(G) and ccghost(G) for the ghost fields $c$ and $\bar c$ in Lagrangian terms and in let statements.

Table 1 shows Feynman rules generated by LanHEP in LaTeX format after processing the input file presented in Fig. 2. Four gluon vertex rule is indicated in the last line. Note that the output in CompHEP format has no 4-gluon vertex explicitly; it is expressed effectively through 3-leg vertices by a constant propagator of some auxiliary field (see section 9 for more details).

Higgs sector of the Standard Model

Figure 3: Input file for the Higgs sector of the Standard Model

The third example illustrates using the multiplets in the framework of LanHEP. Let us consider the Higgs sector of the Standard Model. The Higgs doublet can be defined as

$$\Phi = \left( \begin{array}{c} -iW^+_f\\ (\frac{2M_W}{es_s}+H+iZ_f)/\sqrt{2}\end{array}\right),$$

where $s_w$ is the sinus of the weak angle, $H$ is the Higgs field, $Z_f$ and $W^\pm_f$ are goldstone bosons corresponding to $Z$ and $W^\pm$ gauge fields. The self-interaction of Higgs field read as

$${\cal L}_H= -2\lambda(\Phi\Phi^*-\upsilon^2/2)^2,$$

where $\lambda=(gM_H/M_W)^2/16$, and the vaccuum expectation value $\upsilon=2M_W/g$ (here and below $g=e/s_w$, $g'=e/c_w$.)

The gauge interaction of a Higgs doublet is given by the term $(D_\mu\Phi)(D^\mu\Phi)^*$, where

$$D_\mu = \partial_\mu +ig'B_\mu/2 + ig\vec \tau \vec W_\mu.$$

Here $B$ is $U(1)$ singlet and $W$ is $SU(2)$ triplet,

$$B_\mu=-s_wZ_\mu+c_wA_\mu,\;\;\;\;\; W_\mu^a=\left( \begin{ar... ... W^+_\mu\\ c_wZ_\mu+s_wA_\mu\\ W^-_\mu \end{array}\right),$$

and $\vec\tau$ is the vector $(\tau^+, \tau^3, \tau^-)$.

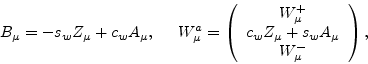
The above model can be represented by the LanHEP code shown in Table 3.

New features in this example include the definition of special symbols for coupling constants $g$, $g'$, gauge and Higgs fields, and the covariant derivative by means of let statement. Note that in the declaration for the fields we have used dummy indices (vector and isospin). The multiplets are defined by the components in the curly brackets.

Note that the option gauge in the declaration of gauge fields allows to use the name gsb(Z) and gsb('W+') for the goldstone bosons.

Table 2: LanHEP output: Feynman rules for Higgs self-interaction

Fields in the vertex	Variational derivative of Lagrangian by fields
${H}_{}$ ${H}_{}$ ${H}_{}$	$-\frac{3}{2}\frac{ e MH{}^2 }{ M_W s_w}$
${H}_{}$ $W^+_F{}_{}$ $W^-_F{}_{}$	$-\frac{1}{2}\frac{ e MH{}^2 }{ M_W s_w}$
${H}_{}$ $Z_F{}_{}$ $Z_F{}_{}$	$-\frac{1}{2}\frac{ e MH{}^2 }{ M_W s_w}$
${H}_{}$ ${H}_{}$ ${H}_{}$ ${H}_{}$	$-\frac{3}{4}\frac{ e{}^2 MH{}^2 }{ M_W{}^2 s_w{}^2 }$
${H}_{}$ ${H}_{}$ $W^+_F{}_{}$ $W^-_F{}_{}$	$-\frac{1}{4}\frac{ e{}^2 MH{}^2 }{ M_W{}^2 s_w{}^2 }$
${H}_{}$ ${H}_{}$ $Z_F{}_{}$ $Z_F{}_{}$	$-\frac{1}{4}\frac{ e{}^2 MH{}^2 }{ M_W{}^2 s_w{}^2 }$
$W^+_F{}_{}$ $W^+_F{}_{}$ $W^-_F{}_{}$ $W^-_F{}_{}$	$-\frac{1}{2}\frac{ e{}^2 MH{}^2 }{ M_W{}^2 s_w{}^2 }$
$W^+_F{}_{}$ $W^-_F{}_{}$ $Z_F{}_{}$ $Z_F{}_{}$	$-\frac{1}{4}\frac{ e{}^2 MH{}^2 }{ M_W{}^2 s_w{}^2 }$
$Z_F{}_{}$ $Z_F{}_{}$ $Z_F{}_{}$ $Z_F{}_{}$	$-\frac{3}{4}\frac{ e{}^2 MH{}^2 }{ M_W{}^2 s_w{}^2 }$

Table 3: LanHEP output: Feynman rules for Higgs gauge interaction

Fields in the vertex	Variational derivative of Lagrangian by fields
${A}_{\mu }$ $W^+{}_{\nu }$ $W^-_F{}_{}$	$i e M_Wg^{\mu \nu}$
${A}_{\mu }$ $W^+_F{}_{}$ $W^-{}_{\nu }$	$- i e M_Wg^{\mu \nu}$
${A}_{\mu }$ $W^+_F{}_{}$ $W^-_F{}_{}$	$- e\big(p_2^\mu -p_3^\mu \big)$
${H}_{}$ $W^+{}_{\mu }$ $W^-{}_{\nu }$	$\frac{ e M_W}{ s_w}g^{\mu \nu}$
${H}_{}$ $W^+{}_{\mu }$ $W^-_F{}_{}$	$-\frac{1}{2}\frac{ i e}{ s_w}\big(p_1^\mu -p_3^\mu \big)$
${H}_{}$ $W^+_F{}_{}$ $W^-{}_{\mu }$	$\frac{1}{2}\frac{ i e}{ s_w}\big(p_2^\mu -p_1^\mu \big)$
${H}_{}$ ${Z}_{\mu }$ ${Z}_{\nu }$	$\frac{ e M_W}{ c_w{}^2 s_w}g^{\mu \nu}$
${H}_{}$ ${Z}_{\mu }$ $Z_F{}_{}$	$-\frac{1}{2}\frac{ i e}{ c_w s_w}\big(p_1^\mu -p_3^\mu \big)$
$W^+{}_{\mu }$ $W^-_F{}_{}$ ${Z}_{\nu }$	$-\frac{ i e M_W s_w}{ c_w}g^{\mu \nu}$
$W^+{}_{\mu }$ $W^-_F{}_{}$ $Z_F{}_{}$	$\frac{1}{2}\frac{ e}{ s_w}\big(p_3^\mu -p_2^\mu \big)$
$W^+_F{}_{}$ $W^-{}_{\mu }$ ${Z}_{\nu }$	$\frac{ i e M_W s_w}{ c_w}g^{\mu \nu}$
$W^+_F{}_{}$ $W^-{}_{\mu }$ $Z_F{}_{}$	$\frac{1}{2}\frac{ e}{ s_w}\big(p_1^\mu -p_3^\mu \big)$
$W^+_F{}_{}$ $W^-_F{}_{}$ ${Z}_{\mu }$	$-\frac{1}{2}\frac{ (1-2 s_w {}^2) e}{ c_w s_w}\big(p_1^\mu -p_2^\mu \big)$
${A}_{\mu }$ ${A}_{\nu }$ $W^+_F{}_{}$ $W^-_F{}_{}$	$2 e{}^2 g^{\mu \nu}$
${A}_{\mu }$ ${H}_{}$ $W^+{}_{\nu }$ $W^-_F{}_{}$	$\frac{1}{2}\frac{ i e{}^2 }{ s_w}g^{\mu \nu}$
${A}_{\mu }$ ${H}_{}$ $W^+_F{}_{}$ $W^-{}_{\nu }$	$-\frac{1}{2}\frac{ i e{}^2 }{ s_w}g^{\mu \nu}$
${A}_{\mu }$ $W^+{}_{\nu }$ $W^-_F{}_{}$ $Z_F{}_{}$	$-\frac{1}{2}\frac{ e{}^2 }{ s_w}g^{\mu \nu}$
${A}_{\mu }$ $W^+_F{}_{}$ $W^-{}_{\nu }$ $Z_F{}_{}$	$-\frac{1}{2}\frac{ e{}^2 }{ s_w}g^{\mu \nu}$
${A}_{\mu }$ $W^+_F{}_{}$ $W^-_F{}_{}$ ${Z}_{\nu }$	$\frac{ (1-2 s_w {}^2) e{}^2 }{ c_w s_w}g^{\mu \nu}$
${H}_{}$ ${H}_{}$ $W^+{}_{\mu }$ $W^-{}_{\nu }$	$\frac{1}{2}\frac{ e{}^2 }{ s_w{}^2 }g^{\mu \nu}$
${H}_{}$ ${H}_{}$ ${Z}_{\mu }$ ${Z}_{\nu }$	$\frac{1}{2}\frac{ e{}^2 }{ c_w{}^2 s_w{}^2 }g^{\mu \nu}$
${H}_{}$ $W^+{}_{\mu }$ $W^-_F{}_{}$ ${Z}_{\nu }$	$-\frac{1}{2}\frac{ i e{}^2 }{ c_w}g^{\mu \nu}$
${H}_{}$ $W^+_F{}_{}$ $W^-{}_{\mu }$ ${Z}_{\nu }$	$\frac{1}{2}\frac{ i e{}^2 }{ c_w}g^{\mu \nu}$
$W^+{}_{\mu }$ $W^+_F{}_{}$ $W^-{}_{\nu }$ $W^-_F{}_{}$	$\frac{1}{2}\frac{ e{}^2 }{ s_w{}^2 }g^{\mu \nu}$
$W^+{}_{\mu }$ $W^-{}_{\nu }$ $Z_F{}_{}$ $Z_F{}_{}$	$\frac{1}{2}\frac{ e{}^2 }{ s_w{}^2 }g^{\mu \nu}$
$W^+{}_{\mu }$ $W^-_F{}_{}$ ${Z}_{\nu }$ $Z_F{}_{}$	$\frac{1}{2}\frac{ e{}^2 }{ c_w}g^{\mu \nu}$
$W^+_F{}_{}$ $W^-{}_{\mu }$ ${Z}_{\nu }$ $Z_F{}_{}$	$\frac{1}{2}\frac{ e{}^2 }{ c_w}g^{\mu \nu}$
$W^+_F{}_{}$ $W^-_F{}_{}$ ${Z}_{\mu }$ ${Z}_{\nu }$	$\frac{1}{2}\frac{ (1-2 s_w {}^2){}^2 e{}^2 }{ c_w{}^2 s_w{}^2 }g^{\mu \nu}$
${Z}_{\mu }$ ${Z}_{\nu }$ $Z_F{}_{}$ $Z_F{}_{}$	$\frac{1}{2}\frac{ e{}^2 }{ c_w{}^2 s_w{}^2 }g^{\mu \nu}$